Correlazione lineare di Pearson

La correlazione è una misura statistica che indica la tendenza che hanno due variabili (X e Y) a variare insieme. Il concetto di correlazione, però, non ipotizza un nesso di causa-effetto (che si analizza ad esempio con la regressione) ma è legato piuttosto al rapporto che esiste tra due variabili quantitative. La correlazione, infatti, ci permette di affermare se tra due variabili c’è una relazione lineare, ma non che una variabile sia la causa dell’altra.

Quando si parla di correlazione bisogna prendere in considerazione vari aspetti: il tipo di relazione esistente tra due variabili, la direzione della relazione, l’intensità della relazione e la significatività.

Per quanto riguarda il tipo di relazione, essa può essere lineare o non lineare.

• La relazione è di tipo lineare se, rappresentata su assi cartesiani utilizzando lo scatterplot come grafico, questa si avvicina alla forma di una retta.
• La relazione è di tipo non lineare, se rappresentata su assi cartesiani, ha un andamento curvilineo (parabola o iperbole).

Per quanto riguarda la direzione della relazione, questa può essere:

• positiva (i valori delle due variabili crescono insieme);
• negativa (all’aumentare dei valori di una variabile i valori dell’altra decrescono).

Per intensità della relazione intendiamo la “forza” della relazione tra le due variabili, sempre che questa relazione esista. Infine, per significatività intendiamo la verifica dell’ipotesi che la relazione lineare tra le due variabili prese in considerazione si possa estendere a livello di popolazione di riferimento.

Per esprimere la relazione lineare esistente tra due variabili, in termini entità e direzione, si utilizza un coefficiente di correlazione.

Tale coefficiente è standardizzato e può assumere valori compresi tra -1 (perfetta relazione lineare negativa) e 1 (perfetta relazione lineare positiva). Un indice di correlazione pari a 0 indica assenza di relazione lineare tra le due variabili.

Esistono vari tipi di coefficienti di correlazione a seconda del tipo di variabile.

• Per le variabili di tipo quantitativo si usa il coefficiente r di Pearson.
• Per le scale ordinali si usano il coefficiente rho di Spearman o il coefficiente tau di Kendall.
• Per le scale categoriali (dicotomiche) si usa il coefficiente phi.

Anche se sono indici di correlazione differenti, l’interpretazione è la stessa!

Il coefficiente di correlazione “r” ricerca una relazione lineare tra due variabili quantitative.
Il nome completo di questo coefficiente è “coefficiente di correlazione di Pearson” in onore dello statistico Karl Pearson.

Di seguito viene riportata la forma analitica del coefficiente di correlazione r di Pearson.

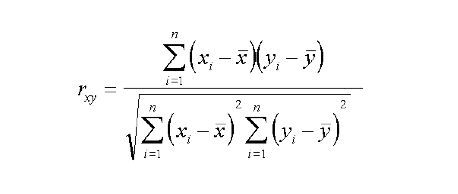
NB: la parola “correlato” non dovrebbe essere usata quando analizziamo la relazione tra variabili qualitative! Per analizzare la relazione tra variabili qualitative utilizziamo il termine associazione e l’indice Chi quadro.

Il coefficiente r ha valori compresi tra –1 e +1 e può essere interpretato (ufficiosamente) come segue:

• se 0,66 < r <= 1 –> forte correlazione positiva
• se 0,33 < r < 0,66 –> moderata correlazione positiva
• se 0 < r < 0,33 –> debole correlazione positiva
• se r = 0 –> nessuna relazione lineare
• se 0 > r > -0,33 –> debole correlazione negativa
• se -0,33 > r > -0,66 –> moderata correlazione negativa
• se -0,66 > r >= -1 –> forte correlazione negativa

Quindi, più il valore è vicino a ± 1, più forte è la relazione.

L’immagine che segue seguito vengono presentati degli esempi di indice di correlazione.

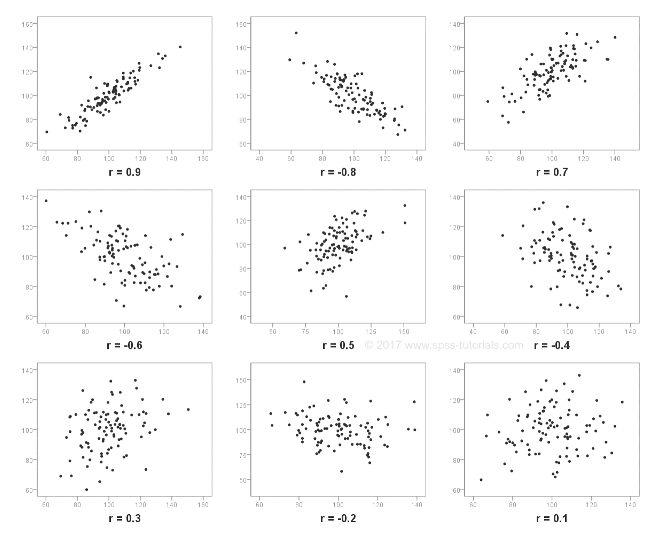
NB: L’indice di correlazione dipende dall’adattamento dei dati alla retta di regressione e non dalla pendenza della retta stimata. Questo vuol dire che se la retta di regressione ha una pendenza elevata, non vuol dire che i dati si adattano a questa!

Per calcolare l’indice di correlazione di Pearson su Excel utilizziamo la funzione = CORREL (X,Y) dove X e Y sono le variabili su cui calcolare l’indice di correlazione.

In Stata, invece, il comando da utilizzare è pwcorr x y. Nel caso in cui volessimo aggiungere la significatività aggiungiamo al comando il termine sig, come mostrato in seguito: pwcorr x y, sig

In R Studio utilizziamo il comando cor (x,y). Se volessimo condurre il test di correlazione, utilizziamo il comando cor.test (x,y).

Ora, vediamo come si calcola l’indice di correlazione di Pearson in SPSS:

• Dal menù analizza selezioniamo Correlazione Bivariata (figura 1).
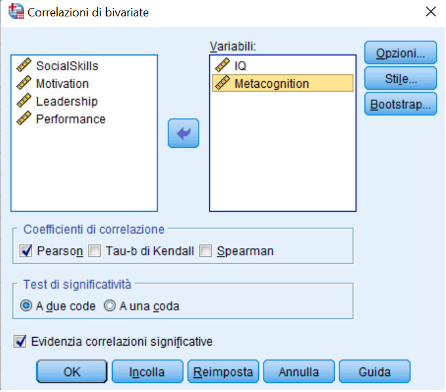
• Una volta selezionata il tipo di correlazione, inserire le variabili su cui calcolare le correlazioni (figura 2).

Figura 1.

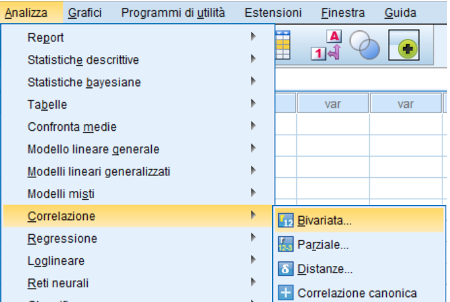
Figura 2.

Per eventuali dubbi o se dovessi aver bisogno di una consulenza professionale non esitare a contattarci!